この記事と同内容の動画
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

 

こんにちは！
逆転の数学、講師の中村です！！

 

７月３０日に「数学検定１級準拠テキスト」が発売されます。
森北出版さんからです。

 

 

実は先日、森北出版さんからメールを頂きました。
「本を送りますので、この新しい問題集を、評価してもらえませんか？」と。

 

僕としては、この動画やブログを見てる方に不利益があるとダメなので。
「率直な評価しかできません。良くない点があればそれも伝えることになりますけど、それでもいいですか？」
と、生意気な返信をしました。

 

すると「もちろんかまわないです。むしろ率直な評価が知りたいのです。」
という旨の返信を頂きました。

 

ので、本が到着し、中身を見終わるのを待って。
今日ここで、紹介する運びとなりました。

 

今回の「数学検定１級準拠テキスト」。
「微分積分」と「線形代数」の２冊がありますが。
まとめて紹介いたします。

 

僕たちが知りたいのは、やっぱり。
「自分に必要かどうか？２千円ずつ払う価値があるかどうか？」ですよね。
ので、その視点で紹介していきたいと思います。

 

「良くない点があれば伝える」なんて生意気なコトを言ったものの。
本が到着するまでの間、amazonを見て、「まぁ絶対当たりやろうな。」と思ってました。

 

というのも、著者は、中村力　先生。
くしくも僕と同じ名字ですが、僕なんか足元にも及ばない大先生です。
各問題の解説を見れば、わかります。

 

中村力先生と、森北出版さんのコンビと言えば。
数検１級を受験されている方なら、ほとんど持っているであろう「数学検定１級実践演習」があります。

 

 

amazonでも高評価です。
もちろん僕も持ってますし、何周もしてます。

 

 

実はこの「数学検定１級実践演習」は。
以前の「数検１級総括：今ならこれで対策する」では紹介しませんでした。
それは、最短距離での合格を重視していたからです。

 

その最短距離も、今回の「数学検定１級準拠テキスト」の発売で、対策はガラリと変わりそうです。
でも、それはまた後日、紹介します。
今回のメインテーマは、「僕たちにとって必要か？２千円の価値があるか？」ですから。

 

で、結論を言うと。
「数学検定１級に合格したいなら、絶対に買う必要がある。」です。

 

理由は３つ。

 

何に重点を置けばいいかがわかる
知っておくべきことを先回りで知れる
二次の問題と詳しい解説がある

 

からです。
詳しく見ていく前に。
それを受けて、「買わなくてもいい人」も先にまとめておきます。

 

・大学数学レベルの微分積分や線形代数はもう完璧で、新たに学ぶコトは何１つもない人
・数検１級の１次試験だけに、最短距離で合格だけできればいい人
・特に試験対策などせず、純粋に自分の数学力だけで勝負したい人

 

これらの人には、不要かと思います。

 

そして注意点は１つ。
「この１冊だけで、０から大丈夫！」というわけではないです。

 

この「数学検定１級準拠テキスト」は、問題集です。
ので、概念はまとめ程度にしかありません。
当然、概念を理解するためには、０からキッチリ解説の参考書が必要になります。

 

その反面、各問題の解説は、素晴らしく詳しくわかりやすいので。
概念のわかる基礎参考書と、この準拠テキストを併用していく。
それで力がついていきます。

 

では改めてここから。
「絶対に買う必要がある理由」を、詳しく見ていきます。

 

・何に重点を置けばいいかがわかる

 

例えば、大学数学の微分積分を学び始める時。
多くの人が、「ε－Ｎ論法」と出会いますよね。

 

またコレが、スッキリいくまでになかなか時間がかかる内容です。
出鼻をくじかれて、「やっぱ、やめとこかな。。。」という気持ちにさえなります。

 

ですが、この準拠テキストでは「ε－Ｎ論法」は取り扱っていません。
数検１級の問題には、（今のところ）不要という判断でしょう。

 

もちろんε－Ｎ論法は、大切な理論です。
ただ数検１級対策だけを考えると、現時点では優先するものではありません。
実際僕は、数時間かけてようやく理解したものの、数検１級では一度も使っていません。
それなら合格してから、ゆとりを持って学習しても、いいですよね。

 

 

準拠テキストでは、数検１級の過去問を中心とした演習問題があります。
そして、これこそ合格のために必要な問題です。
数検は、過去問の類題が繰り返し出題されていますから。

 

 

また、この演習問題の前には例題があります。
もちろん詳しくてわかりやすい解答も、直後にあります。
これが演習問題をスムーズにマスターするための、良い橋渡しになっています。

 

このように例題と演習問題で、効率よく合格力を身につけることができそうです。

 

では、次の理由です。

 

・知っておくべきことを先回りで知れる

 

独学で勉強していると。
「大切な知識なのか？別に知らなくてもいいのか？」
の判断に、どうしても困ります。

 

例えば、行列式の値を求める時に。

 

 

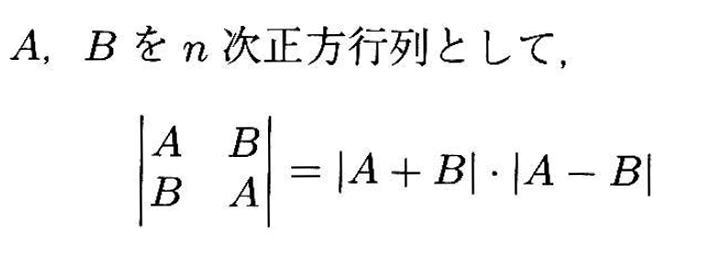
このような便利な公式がありますよね。

 

僕は、この公式に最初出会った時、スル―しちゃいました。
「普通に計算したらいいやん。行列の計算にも慣れるし。」
と思ったからです。

 

でも今では、バンバン使ってます。
（今回の７月試験には、出ませんでしたね。）
１次試験は本当に時間との闘いなので。
この公式で素早く正確に答えを出せば、他の問題に時間を使えるようになります。

 

 

この準拠テキストでは、このような知識を「重要」として紹介してくれています。
大学数学は、ほんと果てしなく広いです。
そんな広い中から、「数検で知っておくべき知識」を先回りして知れる。
これは、合格の大きな助けになってくれます。

 

では最後の理由です。

 

・二次の問題と詳しい解説がある

 

数検の対策で、困ることの１つは二次対策かと思います。
過去問が手に入りにくいからです。

 

 

この準拠テキストでは、演習問題の中に、この二次の問題がたくさんあります。
そして、中村力先生の、丁寧でわかりやすい解説があります。

 

過去問の略解で、ウンウン悶絶してる僕のような人にとっては。
これほどありがたいものはありません。
これだけでも買う価値は、大アリです。

 

以上３つの理由から、「数学検定１級に合格したいなら、絶対に買う必要がある。」と判断します。
だからこそ、買わなくてもいいのは、次のような人です。

 

・大学数学レベルの微分積分や線形代数はもう完璧で、新たに学ぶコトは何１つもない人
⇒微分積分や線形代数に特化した問題集だから

 

・数検１級の”１次試験だけ”（二次は合格済）に、最短距離で合格だけできればいい人
⇒「１次試験だけ合格さえすれば」でいいなら、過去問をできるだけ多く集めて、パターンを意識したテスト練習の方が早いから

 

・特に試験対策などせず、純粋に自分の数学力だけで勝負したい人
⇒「対策なんて邪道だ！合格は自分の数学力の結果論だ！」という方は、ズルしてるような気持ちになるかもしれないから

 

僕自身、ついこの間あった７月の試験で。
合否はわかりませんが、「まだまだ学ぶこと、いっぱいあるな」と痛感しました。
目標は、「何の対策なしでも、一次二次ともに満点合格、死ぬまでには」ですから(笑)

 

テスト中に感じてメモした疑問を解決したら。
この問題集を、最優先でマスターしていこうと思います。
この問題集をマスターしていく中で、自然解決する疑問もいっぱいありそうです。
ただ単に正解させるだけでなく、興味に従って派生させて学び、この１冊ずつを全て味わいつくします。

 

もし買われた人いましたら、ご感想聞かせて頂けたら嬉しいです^^

 

では、数検１級にチャレンジされている方！
これからも共に頑張っていきましょう！！